サヤ取り投資で重要な統計「標準偏差（σ＝シグマ）」

標準偏差（σ＝シグマ）

サヤ取り投資において重要な、もうひとつの統計値が「標準偏差」です。

標準偏差とは、データのバラツキを表す数値です。

一般的にシグマと呼ばれ、バラツキが集まる確率を記号で「σ」と表示します。

この標準偏差もExcelの「STDEV」という関数を使うことで計算できます。

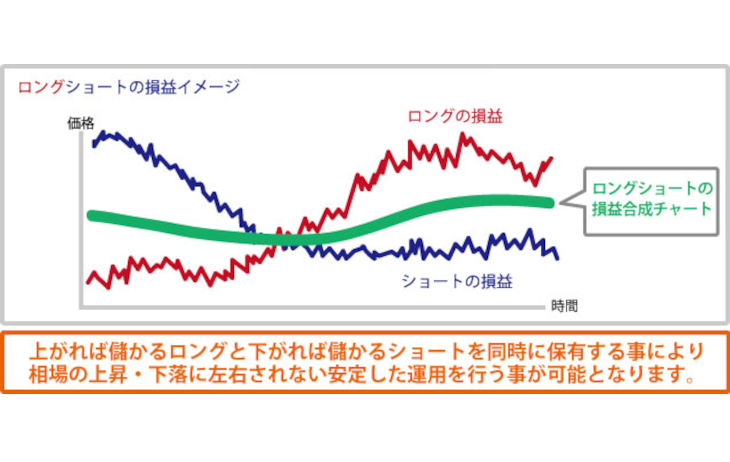
サヤ取り投資を行うときに確認する2銘柄のサヤチャートにおいて、標準偏差は、ボリンジャーバンドとして表示されます。

ボリンジャーバンド（標準偏差）を使うことによって現在の2銘柄のサヤが平常時のサヤの位置と比べて、「現在、どの位置にあるのか」を確認できます。

標準偏差を図で表すと、次ページの上のような正規分布表と呼ばれるものになります。

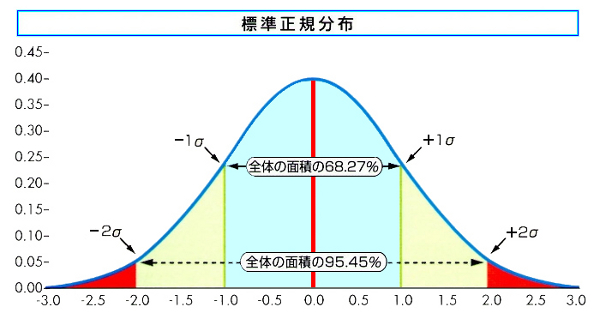
これは、バラついていた全データがこの±1σの範囲内に収まる確率は約68.27％であること、および±2σの範囲内に収まる確率は約95.45％であることを示しています。

ポイントは、±2σの範囲内に収まらない＝確率的に珍しいということです。

相関性の高い2銘柄のサヤは、正規分布する可能性が高いという統計が存在します。

その一方で、過去一定のレンジで推移していたサヤが一時的に大きく離れ、ボリンジャーバンドの±2σをブレイクしていることもあります。

±2σを超えているということは、統計上は4.55％の異常値です。

ここで覚えていただきたいのは、サヤには、異常値である±2σを起点にして「戻ろうとする動き」や「より離れようとする動き」など、いくつかの法則性が存在するということです。

こうした法則性を活かし、サヤの位置をボリンジャーバンドで確認し、実際にサヤ取り投資を行います。

標準偏差の注意点

サヤ取り投資において間違いやすい点は「68.27％」や「95.45％」というパーセンテージの捉え方です。

この数字は、サヤがボリンジャーバンドの±1σや±2σ内に収まる確率を示したものであって、サヤ取り投資の利益になる確率を示したものではありません。

翌日の株価の変動によってボリンジャーバンドの形も日々変形します。

したがって±1σや±2σをブレイクした後にサヤがバンド内に戻ったとしても、必ずしも利益にはなっていないこともあり得ます。

株価が大きく変動した事によって、ボリンジャーバンドも大きく広がってしまうからです。

ボリンジャーバンドのシグマの値ではなく、仕掛けを行った時点からの2銘柄のサヤの推移が損益にとっては重要です。この点には注意してください。

【初心者向け】サヤ取り投資入門レポート！サヤ取りの説明から取引実践まで